Cuckoo Hashing

Introduction

Hash tables play an important role in routers and switches because lookups need to done in constant time. Minimal size packets (64 bytes on Ethernet) on a 100 Gb/s link arrive at a rate of once every 6.7 ns. All packet handling (lookup, rewrite of next hop, updating CRC, etc.) must be done within that time. Hash tables satisfy that requirement and they are typically used for exact match lookups, such as the MAC addressing forwarding table or host IP route lookups. In a lightly populated hash table the average lookup time is $O(1)$. However, when the hash table becomes fuller, hash collisions start to play a role and the lookup time becomes $O(n)$, where n in the number of entries in use in the hash table. This is were cuckoo hashing comes into play. A cuckoo hash table has worst case lookup time that is still $O(1)$ even when the hash table is $> 90%$ full.

Simple Hash Table

A hash table H is a dictionary table that stores keys and associated values. The keys come from a large space N. The size (K) of the hash table is much smaller $(K \ll N)$. A hash function h is used to map $N \rightarrow K$, where $h(n) = k$ with $n \in N, k \in K$. The key k and its associated value are stored in the hash table in slot $h(n)$. But because $(K \ll N)$ multiple elements from N can map on the same slot k. This is a hash collision and occurs when $h(n_1) = k = h(n_2)$. The more keys that are stored in the hash table, the larger the probability of hash collisions.

There are a couple of solutions for handling hash collisions. One of them is using a linked list for keys with the same hash value. Another solution is to store the key in the first empty position after the hash position (continuing at the start of the table when reaching the end). This is called linear probing. Both solutions have the disadvantage that the worst case lookup time is $O(n)$ and that is often not suitable for a router or switch.

Hash Collision Probability

What is the probability of a hash collision? There is a hash collision when two elements hash onto the same slot in the hash table. That means that when hashing $E$ elements: $\exists i, j: h(i) = h(j)$, with $i, j \in E$ and $i \ne j$. Calculating the probability goes as follows. Our hash table has size K. What is the probability $P$ that there are no collisions when we hash $n$ elements to $K$? The first hash can take any of the $K$ slots. For the second element there are $K-1$ slots left out of $K$ in order to avoid a collision, so $\frac{K -1}{K}$. Repeating this argument gives: $$P = \frac{K}{K} \cdot \frac{K-1}{K} \cdot \frac{K-2}{K} \cdots \frac{K-(n-2)}{K} \cdot \frac{K-(n-1)}{K} = \frac{K!}{K^n (K-n)!} \tag{1}$$ Calculating this formula is not practical because these factorials are huge numbers. There are several options. Ons of them is to find a good approximation that can be used in calculations. In order to do this, we can write the sequence in an alternative equivalent form: $$P = 1 \cdot (1 - \frac{1}{K}) \cdot (1 - \frac{2}{K}) \cdots (1 - \frac{n-2}{K}) \cdot (1 - \frac{n-1}{K}) \tag{2}$$ Now we can use the Taylor expansion: $$f(x) = f(a) + \frac{f’(a)}{1!}(x-a) + \frac{f’’(a)}{2!}(x-a)^2 + \cdots \tag{3}$$ and use $f(x) = e^{-x}$: $$e^{-x} = e^{-a} + \frac{- e^{-a}}{1!}(x-a) + \frac{e^{-a}}{2!}(x-a)^2 + \cdots \tag{4}$$ Setting $a=0$ gives: $e^{-x} = 1 - x + x^2 + \cdots$. Using this for equation (2) means that we set $x$ to the terms $\frac{1}{K}, \frac{2}{K} \cdots \frac{n-2}{K}, \frac{n-1}{K}$. When $K \gg n$ the Tayler expension can be approximated by $e^{-x} = 1 - x$. This is the case when the hash table is lightly populated. So we can rewrite equation (2) to: $$\begin{eqnarray} P & = & e^{-\frac{1}{K}} \cdot e^{-\frac{2}{K}} \cdots e^{-\frac{n-2}{K}} \cdot e^{-\frac{n-1}{K}} \nonumber \\\ & = & e^{-\frac{1}{K}(1+2+ \dots + (n-2) + (n-1))} \nonumber \\\ & = & e^{-\frac{1}{K}\frac{n(n-1)}{2}} \nonumber \\\ & = & e^{\frac{-n(n-1)}{2K}} \tag{5} \end{eqnarray}$$ This is the probability for no collisions, so the probability of a collision is given by: $$P_{collision} = 1 - e^{\frac{-n(n-1)}{2K}} \tag{6}$$ This is a function that can easily be computed.

Birthday Problem

A well-known application of the formula in the previous section is the birthday problem. It asks the question: in a room with N people, what is the chance that at least two people share the same birthday? This can be calculated with formula (6). We can solve it for 50% chance and $K = 365$: $$\begin{eqnarray} 0.5 & = & 1 - e^{\frac{-n(n-1)}{2 \cdot 365}} \nonumber \\\ e^{\frac{-n(n-1)}{2 \cdot 365}} & = & 0.5\nonumber \\\ \frac{-n(n-1)}{2 \cdot 365} & = & \ln(0.5) \nonumber \\\ -n(n-1) & = & \ln(0.5) \cdot 2 \cdot 365 \nonumber \\\ n & \approx & \sqrt{- \ln(0.5) \cdot 2 \cdot 365} \nonumber \\\ n & \approx & 22 \nonumber \tag{7} \end{eqnarray}$$ So with 22 people in a room there is a 50% chance that at least two people have the same birthday. That is much lower than many people expect. Actually, a simple hash table has a large chance of collisions. Figure 1 shows the collision probability for a hash table of size 32768 without using a linked list or linear probing. When hashing 200 elements the collision probability is already 50%.

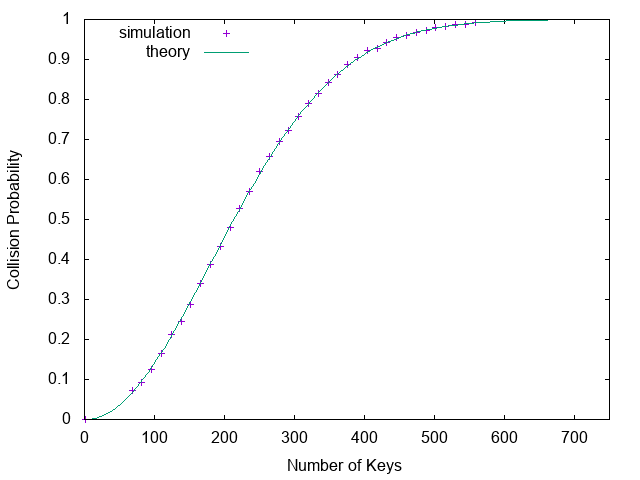
Cuckoo Hashing

In the previous section we saw that a simple hash table, without using linked lists or linear probing, has a very high collision probability. And when using a linked list or linear probing the worst case lookup time becomes $O(n)$, which is a problem in routers and switches. Cuckoo hashing is a solution for this problem. It has a worst case lookup time of $O(1)$. In cuckoo hashing multiple hash functions are used. Each hash function can have its own hash table, but the hash functions can also use the same hash table. When storing an element, each hash function is tried and when it hashes to an empty slot in the table, the element is stored in that slot. When all hashes result in a collision, one of the elements that causes a collision is evicted and the element is stored in that slot. That is why it is called cuckoo hashing. Next we try to store the evicted element with one of the other hash functions, evicting yet another element when there is no empty slot. The eviction process is repeated until the evicted element can be stored in an empty slot. It turns out that cuckoo hashing is very efficient. Only when the hash table is $> 90%$ full the collision probability starts to increase. 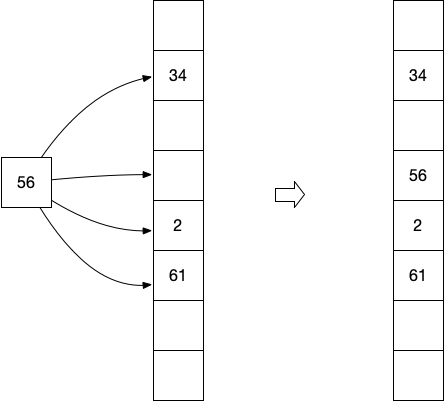The following figures show the cuckoo process. It shows a hash table with four hash functions used for cuckoo hashing. In the first figure the element 56 is inserted in the hash table. Because one of the four hash functions hashes it to an empty slot, it will be stored in that slot.

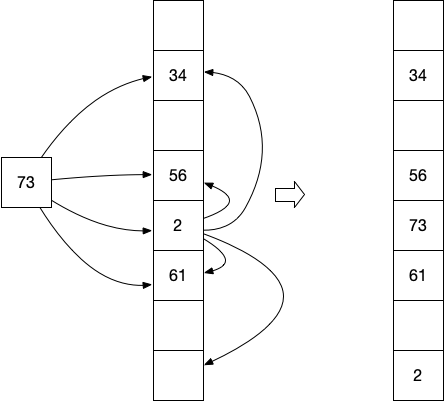
In the second figure the element 73 is inserted in the hash table. All four hash functions hash it to occupied slots. The element 73 is now stored in one of the slots, and the existing element in that slot, 2 in this case, is evicted. The evicted element 2 is now re-inserted in the hash table. Because one of the four hash tables hashes it to an empty slot, it is place in that slot.

Monte Carlo Simulations

A Monte Carlo simulation can be used to generate a probability distribution, such as the hash collision probability. If we want to know what the hash collision probability is when we hash k elements out of a space N, we repeat the hashing of k elements many times and collect the outcomes (hash collision or not). Because I am learning to program in Go, I decided to implement simple and cuckoo hashing in Go. The code can be found in this Github repository. 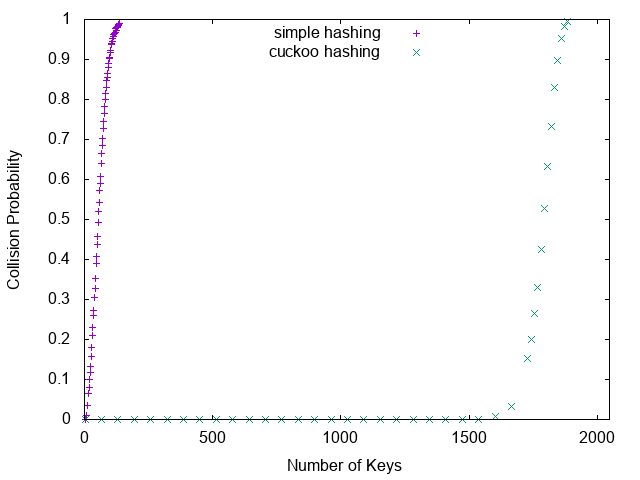The result of simple and cuckoo hashing in a hash table of size 2048 is given in the picture below.